COMMENTARY

Peter Burgess

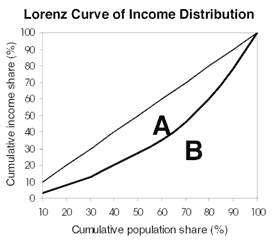
Measuring Inequality

A second definition of welfare which is often considered in analysis is that of ‘relative’ poverty, defined as having little in a specific dimension compared to other members of society. This concept is based on the idea that the way individuals or households perceive their position in society is an important aspect of their welfare. To a certain extent, the use of a relative poverty line in the previous sections does capture this dimension of welfare by classifying as ‘poor’ those who have less than some societal norm.

The overall level of inequality in a country, region or population group – and more generally the distribution of consumption, income or other attributes – is also in itself an important dimension of welfare in that group. Inequality measures can be calculated for any distribution—not just for consumption, income or other monetary variables, but also for land and other continuous and cardinal variables.

Some commonly used measures are presented in Technical Note: Inequality Measures and their Decompositions. For a discussion of the properties and qualities of alternative measures, please consult Inequality: Methods and Tools (177kb PDF), which presents the five key axioms which inequality are usually required to meet. The paper also discusses the calculation of standard errors for usual measures, which is useful for comparisons between estimates of inequality for different distributions.

Gini-coefficient of inequality: This is the most commonly used measure of inequality. The coefficient varies between 0, which reflects complete equality and 1, which indicates complete inequality (one person has all the income or consumption, all others have none). Graphically, the Gini coefficient can be easily represented by the area between the Lorenz curve and the line of equality.

On this figure, the Lorenz curve maps the cumulative income share on the vertical axis against the distribution of the population on the horizontal axis. In this example, 40 percent of the population obtains around 20 percent of total income. If each individual had the same income, or total equality, the income distribution curve would be the straight line in the graph – the line of total equality. The Gini coefficient is calculated as the area A divided by the sum of areas A and B. If income is distributed completely equally, then the Lorenz curve and the line of total equality are merged and the Gini coefficient is zero. If one individual receives all the income, the Lorenz curve would pass through the points (0,0), (100,0) and (100,100), and the surfaces A and B would be similar, leading to a value of one for the Gini-coefficient.

It is sometimes argued that one of the disadvantages of the Gini coefficient is that it is not additive across groups, i.e. the total Gini of a society is not equal to the sum of the Ginis for its sub-groups.

Theil-index: While less commonly used than the Gini coefficient, the Theil-index of inequality has the advantage of being additive across different subgroups or regions in the country. The Theil index, however, does not have a straightforward representation and lacks the appealing interpretation of the Gini coefficient. The Theil index is part of a larger family of measures referred to as the General Entropy class.

Decile dispersion ratio: Also sometimes used is the decile dispersion ratio, which presents the ratio of the average consumption or income of the richest 10 percent of the population divided by the average income of the bottom 10 percent. This ratio can also be calculated for other percentiles (for instance, dividing the average consumption of the richest 5 percent – the 95th percentile – by that of the poorest 5 percent – the 5th percentile). This ratio is readily interpretable, by expressing the income of the rich as multiples of that of the poor.

Share of income/consumption of the poorest x%: A disadvantage of both the Gini coefficients and the Theil indices is that they vary when the distribution varies, no matter if the change occurs at the top or at the bottom or in the middle (any transfer of income between two individuals has an impact on the indices, irrespective of whether it takes place among the rich, among the poor or between the rich and the poor). If a society is most concerned about the share of income of the people at the bottom, a better indicator may be a direct measure, such as the share of income that goes to the poorest 10 or 20 percent. Such a measure would not vary, for example, with changes in tax rates resulting in less disposable income for the top 20 percent at the advantage of the middle class rather than the poor.

It is possible that different measures will rank the same set of distributions in different ways, because of their differing sensitivity to incomes in different parts of the distribution. When rankings are ambiguous, the alternative method of stochastic dominance can be applied. The attached paper Inequality: Methods and Tools (177kb PDF) discusses a type of stochastic dominance which can be used for unambiguous comparisons of inequality across distributions: the mean-normalized second-order dominance, or Lorenz dominance.